Course of Differential Geometry
by Ruslan Sharipov
Publisher: Samizdat Press 2004
ISBN/ASIN: 5747701290
Number of pages: 132
Description:
This book is a textbook for the basic course of differential geometry. It is recommended as an introductory material for this subject. The book is devoted to the firs acquaintance with the differential geometry. Therefore it begins with the theory of curves in three-dimensional Euclidean space E. Then the vectorial analysis in E is stated both in Cartesian and curvilinear coordinates, afterward the theory of surfaces in the space E is considered.
Download or read it online for free here:
Download link
(1MB, PDF)
Similar books
Differential Geometry in Physicsby Gabriel Lugo - University of North Carolina at Wilmington
These notes were developed as a supplement to a course on Differential Geometry at the advanced undergraduate level, which the author has taught. This texts has an early introduction to differential forms and their applications to Physics.
(18947 views)
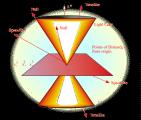Introduction to Differential Geometry and General Relativityby Stefan Waner
Smooth manifolds and scalar fields, tangent vectors, contravariant and covariant vector fields, tensor fields, Riemannian manifolds, locally Minkowskian manifolds, covariant differentiation, the Riemann curvature tensor, premises of general relativity.
(22824 views)
Differential Geometry Course Notesby Richard Koch - University of Oregon
These are differential geometry course notes. From the table of contents: Preface; Curves; Surfaces; Extrinsic Theory; The Covariant Derivative; The Theorema Egregium; The Gauss-Bonnet Theorem; Riemann's Counting Argument.
(12200 views)
Differentiable Manifoldsby Nigel Hitchin
The historical driving force of the theory of manifolds was General Relativity, where the manifold is four-dimensional spacetime, wormholes and all. This text is occupied with the theory of differential forms and the exterior derivative.
(19237 views)